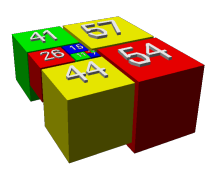
Squaring the Plane
This is the homepage of our research in tiling the plane with
squares.
abstract
We can tile the plane with exactly one of each square of positive
integer side.
You can download the paper and view a short animation (120K), a longer one (532K), or a larger version (1.7M) of the same. The VPython program used to generate the
animations is available by request, but it's still under
development.
open questions
- Is there a "simple" tiling with squares?
- Is there a tiling using just the odd squares?
- Answer (8/06): no. If no two members of a set add to a
third, then there does not exist a tiling of the plane using only
squares with side-length from the set.
- Conjecture: If a set grows faster,
asymptotically, than the Fibonacci numbers, then it can't tile the
plane.
- Can the half-plane or quarter-plane be tiled?
- Is there a three-colorable tiling?
- Is there a tiling with triangles?
- Can the efficiency of the tiling be improved?
- Can space be cubed?